En la busqueda de técnicas para poder dibujar superficies abiertas más complejas como Rostros, Terrenos y por supuesto superfices cerradas que puedan servir como las partes de un humano, como podria ser la cabeza, el torso, las piernas, etc. sin tener que dibujar estas a partir de sus poligonos fundamentales y luego tener que guardar en un archivo todos los puntos xyz, inventé esta forma que puede funcionar como las superficies de Bezier para alterar una superficie a partir de unos puntos de control, y luego de moldear la superficie a tu gusto, solo tienes que guardar los puntos de control.
A continuación describiremos mi idea a partir de la matemática que la soporta y yo llamo "Dibujo mediante la función de Gauss".
En unos dias subire el código fuente para que puedan ver el resultado de todo esto.
Mientras tanto les adelanto unas imagenes de los resultados obtenidos usando esta técnica que yo idee a partir de la Función de Gauss:
Sustentación:
A continuación describiremos mi idea a partir de la matemática que la soporta y yo llamo "Dibujo mediante la función de Gauss".
En unos dias subire el código fuente para que puedan ver el resultado de todo esto.
Mientras tanto les adelanto unas imagenes de los resultados obtenidos usando esta técnica que yo idee a partir de la Función de Gauss:
 |
| Esta cabeza esta formada a partir de la esfera que se ve en el fondo. El punto negro que se ve en la nariz, es uno de los puntos de control usados para dibujar este rostro. |
Sustentación:
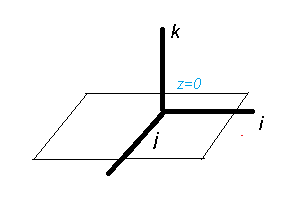
La Superficie básica es un plano. Supongamos el plano z=0.
Dibujo de Superficies Abiertas:
Para empezar a dibujar en OpenGL se suele usar como ejemplos figuras geométricas básicas como Triángulos, o Cubos.
A continuación vamos a describir una forma básica en la que podemos dibujar Superficies y controlar la forma de las mismas.
Una función útil para deformar este plano es superponiéndole la función Gaussiana, conocida también como la campana de Gauss:
En donde:
- a es una constante positiva o negativa que define la altura de la campana,
- b es una constante que define el ancho de la campana
- x0 es una constante que define la posición de la campana
Como se ve esta función nos permite definir una deformación controlada (amplitud y dispersión) en un punto x0 del el espacio.
La versión en el espacio de tres dimensiones de la campana de Gauss es la siguiente:
En donde:
- a es una constante positiva o negativa que define la altura de la campana,
- bx y by son constantes que definen la dispersión de la deformación tanto en el sentido del eje x (i) o del eje y(j).
- x0 y y0 definen los puntos en el plano z=0 donde va a estar la cumbre de la deformación.
De esta forma se puede ver la deformación en el plano z=0 producto de la campana de Gauss.
Sin embargo esta deformación solo se puede proyectar en el eje Z (k). Para poder proyectarla en todos en el sentido de X, Z, Y debemos expresar el plano como una función vectorial de la siguiente forma:
Con esta nueva función se puede inclinar la deformación en cualquiera de los ejes del plano.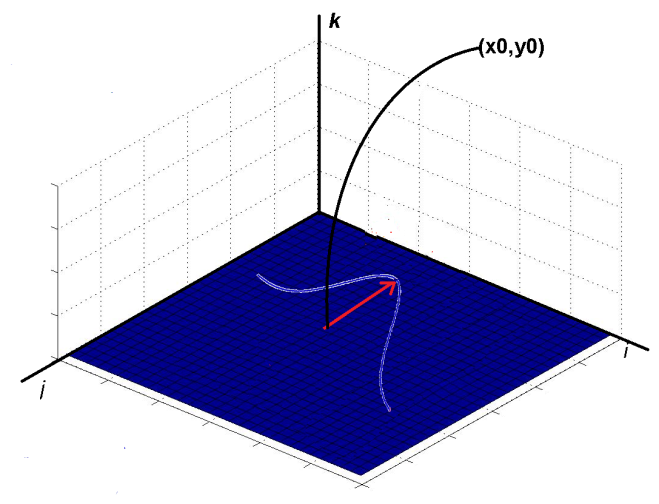
Ahora podemos moldear como si se tratara de masilla el plano z=0 al superponer varias deformaciones independientes.
En esta sumatoria n es el total de deformaciones aplicadas al plano. Por cada deformación los puntos de control son los ya mencionados:
- axi, ayi, azi, son constantes positivas o negativas que define la magnitud de la deformación en el eje x (i), eje y(j), eje z(k) respectivamente.
- bx y by son contantes que definen la dispersión de la deformación tanto en el sentido del eje x (i) o del eje y(j).
- x0 y y0 definen los puntos en el plano z=0 donde va a estar la cumbre de la deformación.
Así se pueden obtener formas libres como Aletas, e incluso mediante deformaciones contiguas solapadas se pueden dar forma inclusive a un rostro humano:
Obtención de Vectores Normales:
El cálculo de vectores normales unitarios por cada vértice de la superficie es necesario para que se pueda realizar la iluminación de la superficie mediante el algoritmo de Lambert.
Por forma vectorial en la que hemos expresado la superficie, sabemos que:
Calculamos las derivadas parciales de la siguiente forma:
El vector normal unitario de
y se obtiene dividiendo N Por su módulo, Esta representación no la haremos de forma simbólica, más bien recomendamos evaluar por cada vértice las derivadas parciales y realizar el producto cruz, y la división de su módulo con los valores específicos.
Dibujo de Superficies Cerradas:
Unir superficies abiertas para formar cuerpos sólidos puede resultar un poco complicado.
Resulta conveniente usar una figura geométrica primitiva como base para construir superficies cerradas, en este caso usaremos una esfera de radio uno en el origen.
La ecuación de una esfera en el espacio:
Cada punto en espacio de la superficie de una esfera puede ser definido usando las coordenadas esféricas (r, ϕ, θ) mediante la siguiente ecuación vectorial:
S(θ,φ)=(rsin θcos φ )i+(rsin θsin φ )j+(rcos θ )k
Donde 0≤θ≤π y 0≤φ≤2π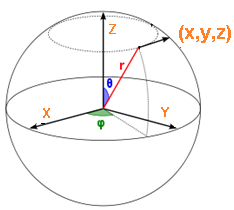
La constante r es el radio de la esfera, y (θ, ϕ) son los parámetros angulares de la esfera (Variables). Para poder manipular la forma de esta esfera, debemos Sumar a cada una de las funciones paramétricas las funciones paramétricas de las deformaciones.
Esto es igualar los parámetros de entrada de las ecuaciones de las deformaciones con los de la esfera unitaria: x = ϕ ; y = θ y sumar ambas funciones vectoriales dejando por resultante la siguiente función vectorial:
Esto es el equivalente al envolver la esfera con la superficie abierta deformada:
Obtención de Vectores Normales:
Para obtener el vector normal usamos nuevamente la formula: N=∂S∂x×∂S∂y , Ya tenemos las derivadas parciales para las ecuaciones paramétricas de las deformaciones así que solo calcularemos las derivadas parciales de la esfera:
S(φ,θ)=(rsin θcos φ )i+(rsin θsin φ )j+(rcos θ )k
∂S(φ,θ)∂θ=r(cos θ cos φ )i+r(cos θ sin φ )j-(rsin θ )k
∂S(φ,θ)∂φ=-r(sin θ sin φ )i+r(sin θ cos φ )j
Dando por resultado las siguientes derivadas parciales:
